Contents
これまでの2次方程式の解き方
新しい解き方が気になるところだと思いますが、一応これまでのおさらいをしておきましょう。現在のカリキュラムでは、中学生3年生で2次方程式の解き方を学んでいますが、以下に示す4種類の解法を中学3年生は学習しています。実際に使うことが多いのは、因数分解による方法で、それが使えない場合は、解の公式を使用するのが一般的だと思います。
平方根による解き方
2乗を取る場合に±√をつけて表す方法です。
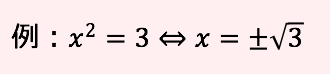
因数分解による解き方
この問題では、かけて−3たして−2になるペアを探して因数分解します。
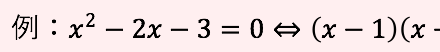
平方完成による解き方
2次関数のグラフの頂点を求める際につかいます。中学生はあまり使わないのでやり方を聞くと答えられない生徒が多いです。
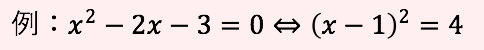
解の公式による解き方
覚えた公式に2次方程式を当てはめて解く方法です。因数分解できない場合でも解くことができます。
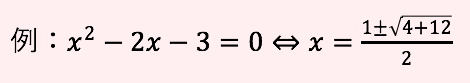
2次方程式の新しい解き方
新しい解き方を考案した人
2次方程式の新しい解き方を考案したのが、アメリカのカーネギーメロン大学に勤める数学の教授、ポー・シェン・ロー(Po-Shen Loh)さんです。彼は、現在、アメリカの国際数学オリンピックチームのナショナルコーチもつとめています。
2次方程式の新しい解き方(方法)


となります。本当かどうかきになる人は、解の公式でといてみてください。
2次方程式の新しい解き方の利点
ほとんどの学習者が因数分解で解けないものは解の公式を用いて解いていると思いますが、それに対して、ポー・シェン・ロー(Po-Shen Loh)さんは論文中で次のように言っています。
However, it is unfortunate that for billions of people worldwide, the quadratic formula is also their first experience of a rather complicated formula which they memorize.
世界中の40億の人にとって、2次方程式が、かなり複雑な公式の暗記の初めての経験になる
https://arxiv.org/pdf/1910.06709.pdf
2次方程式の解の公式による負担以外にも新しい解き方には以下のような利点があるといっています。
- 解の公式のように、理解していない公式に数を代入していくのではなく、単純な論理的ステップで解を導くことができる
- 解と係数の関係を示す機会にもなる
- 平方完成による解き方は新しく、主に3つのステップを実行していくが、それと比べて因数分解による解法を学習した流れで、それを置き換える形で解くことができる
新しい解き方で生徒に教えてみたくなってきましたか?ぜひお試しください。